🚩변산성(variability) - 자료의 분포에 대한 정보 제공
- 편차(deviation): 각 데이터가 평균으로부터 떨어진 정도 (데이터-평균)
- 분산(variance): 편차 제곱들의 평균
- 표준편차(standard deviation): 분산의 제곱근
| ℹ️ 변산성(variability), 분산도(variation), 분산(variance) 차이? 변산성(variability): 범위, 분산, 표준편차와 같이 자료의 분포에 대한 정보를 제공하는 측정치라고 할 수 있다. 분산(variance): 위와 같이 편차 제곱들의 평균을 의미한다. 분산도(variation): 분포의 흩어진 정도를 말한다. 즉, 다양성의 정도를 나타낸다. 분산도 또는 변산이라고 말하기도 한다. 변산성(variability)과 분산도(variation)의 차이는 찾아도 잘 안 나오던데, 둘은 같은 의미라고 생각된다. 분산도는 분포의 특성을 알기 위해 고려하는 중심경향값과 같이 분포의 특성을 알기 위해 알고자 하는 분포의 흩어진 정도를 의미한다. 즉, 해당 데이터에서 데이터가 얼마나 퍼져있는가를 의미하고 변산성도 이와 같은 개념이기 때문에 변산을 확인하기 위해 해당 데이터의 범위, 사분위 편차, 분산, 표준편차 등을 계산하여 확인할 수 있다. *variability, variance - 사회과학을 위한 고급 통계학(김청택 저)에서 발췌 *variation - 현대기초통계학 이해와 적용(성태제 저)에서 발췌 |
분산과 표준편차를 공식으로 이미 많이 알고 있을 것이다.
그런데 분산과 표준편차는 대체 왜 필요한 것일까?
이들 값이 가지는 의미가 무엇일까? 평균은 익숙한데 분산, 표준편차는 직관적으로 잘 와닿지 않는다.
우선, 평균은 데이터를 대표하는 수치이다. 최빈치, 중앙값과 함께 대푯값 중 하나이다.
평균에서는 자료들이 얼마나 흩어져 있는지에 대한 정보를 알 수 없다.
똑같이 평균이 5인데 흩어진 정도가 다를 수 있다.
예를 하나 들어 보자.
A반과 B반의 중간고사 성적 평균이 50점(100점 만점)으로 같다고 하자.
이 정보만 보고 A반과 B반 실력이 같다고 이야기할 수 있을까? 좀 더 정확하게는, A반과 B반 학생들의 실력이 비슷하게 구성되어 있겠다고 생각할 수 있을까?
A반과 B반 데이터가 아래와 같다면. A, B반에 대해서 어떻게 말할 수 있을 것인가?
| A반 | 10 | 20 | 50 | 80 | 90 |
| B반 | 45 | 47 | 50 | 53 | 55 |
A반은 개개인마다 차이가 큰데 비해 B반은 차이가 별로 없고 중위권 학생들만 모여 있는 고만고만한 반이라고 볼 수 있다.
표준편차를 살펴보면 A반은 35.36점, B반은 4.21점이다.
표준편차는 데이터가 퍼져 있는 정도(불규칙한 상태, 개개인의 차이)가 어느 정도인지를 말해준다.
같은 평균 50점이더라도 표준편차가 큰 경우, 데이터 각각이 서로 차이가 많이 난다고 볼 수 있다.
대략적으로 왜 표준편차가 필요한지 감이 온다면,
편차, 분산, 표준편차를 각각 자세히 살펴보자.
✏️편차(deviation)
편차는 자료가 평균으로부터 떨어진 정도를 말한다.

수식으로는 (데이터-평균)이다.
데이터가 흩어진 정도는 평균적으로 각각의 자료들이 평균으로부터 떨어진 정도가 어떻게 되는가를 의미한다.
그럼 편차들의 평균을 쓰면 되겠다고 생각하게 된다.
그렇지만 편차들의 평균에는 문제가 하나 있다.
편차들의 합이 항상 0이 되기 때문이다. 그럼 자료가 분명히 제각각 다르게 흩어져 있는데도 편차들의 평균은 0이 된다. 0이 된다는 말은 데이터가 흩어진 정도가 0, 점수들이 흩어져 있지 않는다=모든 사례 수 값이 같다는 결과가 나온다.
이런 문제 때문에 편차들을 제곱하여 합한 값들을 평균내어 분산이라는 통계량을 만들어내는 것이다.
✏️분산(variance) = 변량(교육학, 교육심리학에서는 변량이라고 하기도 함)
분산은 편차를 자승하여 모두 합한 것을 총 사례 수로 나눈 값이다.
표기: s2 (표본 통계량) 또는 𝜎2 (모수치)

분산은
왜 편차에 절대값을 씌워 평균내면 안 되는가? 라는 질문이 들 수 있다.
단순하게 예시에 나온 데이터만 보면 편차 절댓값의 평균을 구하면 쉽다고 생각할 수 있는데, 절대값은 계산할 때 수학적으로 복잡해지는 문제가 있다. (예를 들어, y= |x-a| 가 있다고 하면 (x≥a), (x<a)라는 조건으로 식을 풀어야 하기 때문이다. 사실 이렇게 얘기해준 사람은 없고, 수학적 계산이 복잡해진다고만 들었는데, 편차에 절댓값을 씌워 평균을 구하는 것이 왜 안 되는지 나름대로 내가 이해한 방식이다...)
분산에도 문제가 2가지 있는데, 1) 흩어져 있는 상태를 나타내는 수치로는 너무 크다는 것, 2) 단위가 변한다는 것 이다.
그래서 분산에 표준편차를 씌워 이 문제를 해결하게 된다.
✏️표준편차(standard deviation)
표준편차는 분산의 제곱근이다.
표기: s (표본 통계량) 또는 𝜎 (모수치)
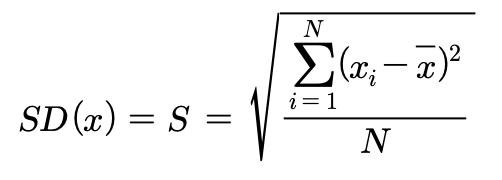
variability, variation, variance 와 같이 헷갈리는 용어들에 대한 정리를 하였고,
편차, 분산, 표준편차의 개념과 필요성에 대해 살펴보았다.
2편에서는 표준편차를 어떻게 이해하고 받아들이면 되는지 이야기해보려고 한다.
'대학원 > 기초통계' 카테고리의 다른 글
| 표집 방법/표본 추출법 sampling method (0) | 2023.05.15 |
|---|---|
| [기초통계] 신뢰도와 타당도 (feat. 필요조건과 충분조건 개념) (0) | 2023.05.08 |
| [기초통계] 기술통계 & 추리통계 개념 (0) | 2023.05.03 |
| 통계 개념 (한/영) (last update: 23. 5. 27.) (0) | 2023.05.02 |
| 분포 - 정규분포, t분포, 카이제곱분포, F분포 (수정중) (0) | 2023.04.19 |